机器学习中最基本的问题就是二元分类问题和回归问题。你如果设计了一个分类模型或者回归模型,如何刻画你这个模型的好坏呢?就要用到这些性能指标了。
分类
最基本的分类是二元分类,就是说数据输入你的模型,你告诉人家这是某种object还是不是。分类,必然存在正确的情形,也存在错误的情形。对于二元分类,就是说,正确的情形包括正类预测为正类,负类预测为负类;错误的情形当然包括将正类预测为负类,将负类预测为正类。学术界用混淆矩阵刻画这个结果:
混淆矩阵
True Positive(真正, TP):将正类预测为正类数.
True Negative(真负 , TN):将负类预测为负类数.
False Positive(假正, FP):将负类预测为正类数 误报 (Type I error).
False Negative(假负 , FN):将正类预测为负类数 漏报 (Type II error).
为什么称之为矩阵呢?因为经常这样记录这四个数:
| | positive | negative |
| :—–: | :——: | :——: |
| True | True Positive(TP) | True Negative(TN) |
| False | False Positive(FP) | False Negative(FN) |
在这个混淆矩阵基础上,产生了几个性能指标:
准确率(Accuracy)
$$ACC=\frac {TP+TN}{TP+TN+FP+FN}$$
在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量是很少的,一般只有千分之几,如果用acc,即使全部预测成负类(不点击)acc 也有 99% 以上,没有意义。
精确率(Precision)
$$P={TP \over TP+FP}$$
召回率(Recall)
有的文献称之为sensitivity,true positive rate
$$R=\frac {TP}{TP+FN}$$
在信息检索领域,精确率和召回率又被分别称为查准率和查全率。
$$查准率=\frac{检索出的相关信息量}{检索出的信息总量}, 查全率=\frac{检索出的相关信息量}{系统中的相关信息总量}$$
F1值(F1 Score)
精确率和召回率的调和均值。所谓调和均值,就是倒数平均数,是总体各统计变量倒数的算术平均数的倒数。看公式:
$${2 \over F_1}={1 \over P} + {1 \over R} $$
可以很容易推出:
$$F_1={2PR \over {P+R}}={2TP \over {2TP+FP+FN}}$$
精确率和准确率都高的情况下,F1 值也会高。
PR曲线
PR曲线指Precision-Recall曲线,中文为查准率-查全率曲线。
对于一个分类器(也就是一种分类算法啦),可以给出每个样本属于正类的概率。你可以选择一个阈值,将概率大于这个阈值的归为正类,其他归为负类。因此,一个阈值对应一个划分,也就对应一个(Recall,Precision)pair。选择不同的阈值,得到很多的pairs。在Recall-Precision坐标系,一个pair对一个点,把这些点连接起来就构成PR曲线。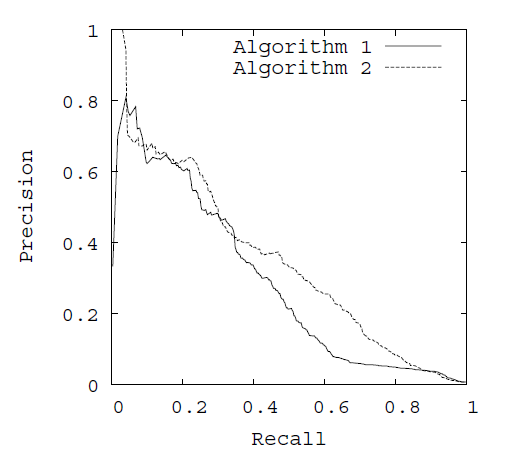
通常随着分类阈值从大到小变化(大于阈值认为属于正类),查准率减小,查全率增加。比较两个分类器好坏时,显然是查得又准又全的比较好,也就是的PR曲线越往坐标(1,1)的位置靠近越好。
ROC 曲线
先讨论几个指标:TPR,FPR,TNR
(1) TPR(True Postive Rate)
真正类率,代表分类器预测的正类中实际正实例占所有正实例的比例,也就是前文中的Recall。有的文献称为敏感度(Sensitivity)。
$$TPR=\frac {TP}{TP+FN}$$
(2) TNR(True Negative Rate)
真负类率,代表分类器预测的负类中实际负实例占所有负实例的比例,又称为特异度(Specificity)
$$TNR=\frac {TN}{FP+TN}$$
(3) FPR(False Postive Rate)
假正类率,代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity
$$FPR={FP \over FP+TN}$$
显然,TNR+FPR=1。

正如我们在这个ROC曲线的示例图中看到的那样,ROC曲线的横坐标为false positive rate(FPR),纵坐标为true positive rate(TPR)。
我们讨论ROC曲线图中的四个点和一条线。
- 第一个点,(0,1),即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0。Wow,这是一个完美的分类器,它将所有的样本都正确分类。
- 第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。
- 第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)。
- 第四个点(1,1),分类器实际上预测所有的样本都为正样本。
- ROC曲线图中的虚线y=x上的点。这条对角线上的点其实表示的是一个采用随机猜测策略的分类器的结果,例如(0.5,0.5),表示该分类器随机对于一半的样本猜测其为正样本,另外一半的样本为负样本。
经过以上的分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好;PR曲线越接近右上角,该分类器性能越好。
那么是怎么得到这个曲线的呢?
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值,这又是如何得到的呢?其实这和得到PR曲线一个原理。
有一个视频讲这个讲得特别好。推荐一下,ROC Curves and Area Under the Curve(AUC) ,如果上不了YOUTUBE,可以去看看视频末尾提到的这个网站ROC-Visualization。
大概原理是这样的。假如你已经有了一个模型,你就可以根据这个模型得到了所有样本的概率输出(属于正样本的概率)。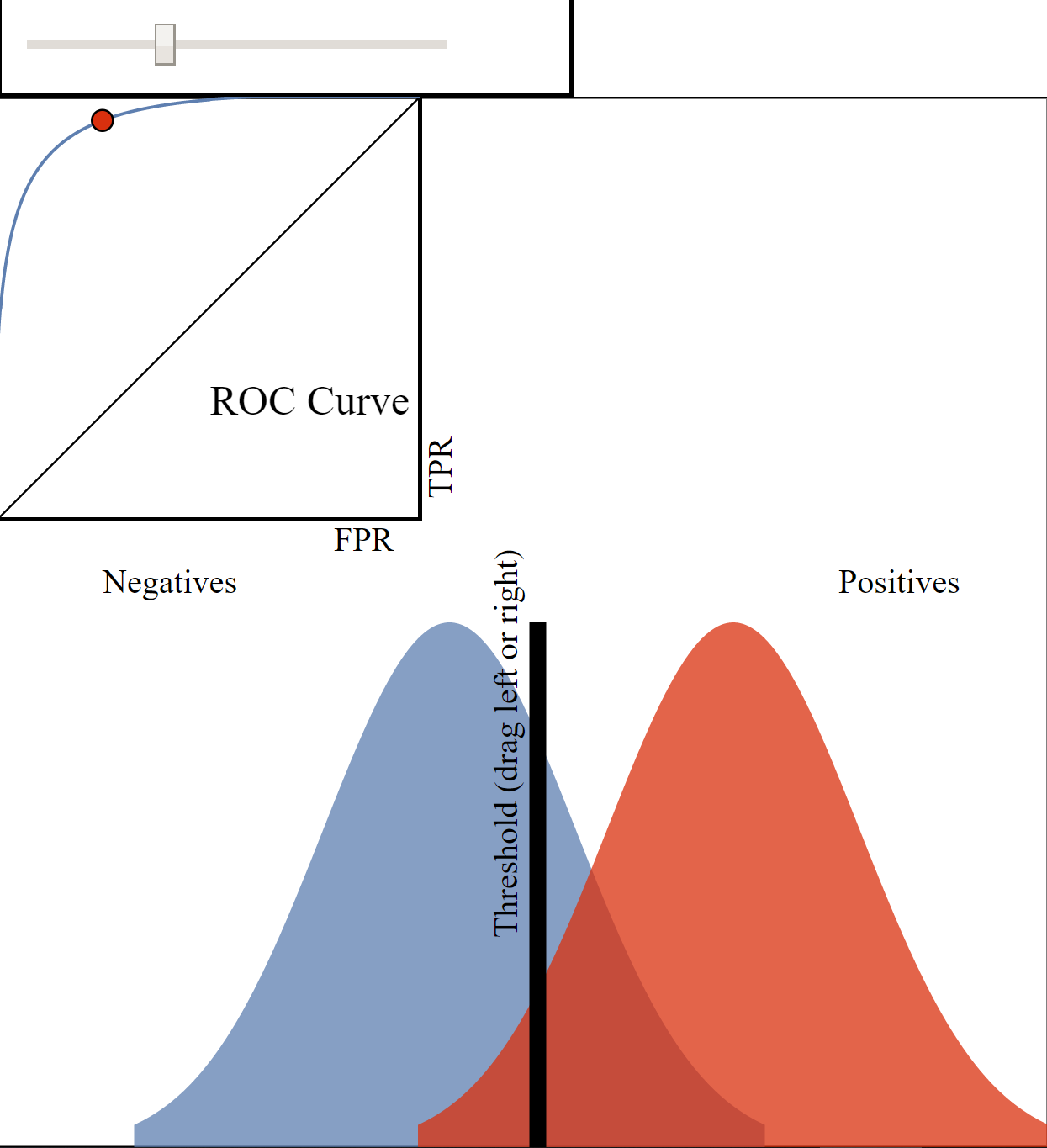
现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。

接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:

当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
其实,我们并不一定要得到每个测试样本是正样本的概率值,只要得到这个分类器对该测试样本的“评分值”即可(评分值并不一定在(0,1)区间)。评分越高,表示分类器越肯定地认为这个测试样本是正样本,而且同时使用各个评分值作为threshold。我认为将评分值转化为概率更易于理解一些。
为什么使用ROC曲线
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线5的对比:
AUC(Area Under Curve)
AUC被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。
根据(Fawcett, 2006),AUC的值的含义[^FAWCETT2006]是:
The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
什么意思呢?随机挑选一个正样本和一个负样本,根据当前的分类算法,计算得到两个样本的Score值。正样本得分比负样本得分高的概率就是AUC值。
简单说:AUC值越大的分类器,正确率越高[^AUC&ROC]。
分析一下:
(1) AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
(2) 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
(3) AUC=0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
(4) AUC<0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测,因此不存在 AUC<0.5 的情况。
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。

在了解了ROC曲线的构造过程后,编写代码实现并不是一件困难的事情。相比自己编写代码,有时候阅读其他人的代码收获更多,当然过程也更痛苦些。在此推荐scikit-learn中关于计算AUC的代码。
在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
说明,文中除了第一张图来自Wikipedia外,其他的图都来自论文(Fawcett, 2006)6截图.
引用及其他链接:
维基百科中对ROC的介绍: http://en.wikipedia.org/wiki/Receiver_operating_characteristic
ROC曲线及AUC评价指标 by 冒泡的崔:http://bubblexc.com/y2011/148/
我避免将precision,recall等评价指标翻译成中文,因为它们可能对应多个中文解释,极易产生混淆。 ↩
图片来源:http://en.wikipedia.org/wiki/File:Roccurves.png ↩
这种映射不一定都是可靠的,即你不一定真的得到了某个样本是正样本的概率。 ↩
注意这里使用了“Score”,而不是概率,我们暂且可以认为“Score”值就是是正样本的概率。 ↩
Davis, J., & Goadrich, M. (2006, June). The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd international conference on Machine learning (pp. 233-240). ACM. ↩
[^FAWCETT2006]:Fawcett, T. (2006). An introduction to ROC analysis. Pattern recognition letters, 27(8), 861-874
[^AUC&ROC]: AUC与ROC - 衡量分类器的好坏。